त्रिभुजों की सर्वांगसमता तथा समरूपता, परिभाषा, प्रकार, नियम, कसौटियां तथा अन्तर, उदाहरण एवं चित्र सहित

इस लेख में हमारे द्वारा त्रिभुजों की सर्वांगसमता तथा समरूपता, परिभाषा, प्रकार, नियम, कसौटियां तथा अन्तर, उदाहरण एवं चित्र सहित दिए गए है जो कक्षा 9,10 तथा 11 एवं 12 के लिए अतिमहत्वपूर्ण है | कक्षा 9,10,11,12 NCERT and all exam के लिए तो यह लेख बहुत ही फायदेमंद है | आप हमे नीचे comment करके बता सकते है कि आपको यह लेख कैसा लगा |

{tocify} $title={Table of Contents}

सर्वांगसमता का अर्थ :-

सर्वांगसमता का अर्थ है " सभी प्रकार से बराबर | " अर्थात् वे आकृतियाँ जिनके समान आकार और समान माप है |

सर्वांगसमता (CONGRUENCY) क्या है / सर्वांगसमता किसे कहते है ?

सर्वांगसमता की परिभाषा के अनुसार , दो वस्तुओं के सर्वांगसम होने के सम्बन्ध को सर्वांगसमता कहते है |
दूसरे शब्दों में , यदि एक आकृति को किसी अन्य आकृति पर अध्यारोपित किया जाए और पहली आकृति , दूसरी आकृति को पूर्णतया ढक ले तो इस प्रकार की दोनों आकृतियाँ , सर्वांगसम आकृतियाँ कहलाती है |

सर्वांगसमता के उदाहरण :-

1. एक ही कंपनी के शेविंग ब्लेड
2. एक ही पैकेट के बिस्कुट
3. समान आकार और समान माप के त्रिभुज

सर्वांगसमता का चिन्ह :-

यदि आकृति A तथा B परस्पर सर्वांगसम है तो उन्हें निम्न चिन्ह से व्यक्त करते है -
आकृति A ≌ आकृति B
इसी चिन्ह को सर्वांगसमता का चिन्ह कहते है |

रेखाखण्डों में सर्वांगसमता :-

यदि दो रेखाखण्डों की लम्बाई समान ( बराबर ) है तो वे सर्वांगसम होते है | यदि दो रेखाखण्ड सर्वांगसम है तो उनकी लम्बाईयां समान होती है |
उदाहरण -

यहाँ AB = CD
या AB ≌ CD

कोणों की सर्वांगसमता :-

यदि दो कोणों की माप समान हो तो वे सर्वांगसम होते है तथा यदि दो कोण सर्वांगसम है तो उनकी माप भी समान होती है |

उदाहरण :-

यहाँ ∠ABC = ∠PQR
अर्थात् ∠ABC ≌ ∠PQR
कोणों की सर्वांगसमता पूर्णतया उनके मापों की समानता के ऊपर निर्भर करती है |

त्रिभुजों की सर्वांगसमता की शर्तें :-

दो त्रिभुज सर्वांगसम होते है यदि वे एक - दूसरे की प्रतिलिपियाँ हो और एक को दूसरे के ऊपर रखे जाने पर , वे एक दूसरे को आपस में पूर्णतया ढक ले |
यदि दो त्रिभुज सर्वांगसम है तो उनके संगत भाग ( कोण और भुजाएँ ) समान होते है | इसे संक्षेप में CPCT लिखते है |

∆ABC तथा ∆PQR समान आकार एवं समान आमाप के है ये त्रिभुज सर्वांगसम है |
अत: ∆ABC ≌ ∆PQR

त्रिभुजों की सर्वांगसमता के नियम / प्रतिबंध प्रकार / कसौटियां:-

त्रिभुजों की सर्वांगसमता के मुख्यत: चार नियम या प्रतिबंध सूत्र है जिनका परिभाषा , उदाहरण एवं चित्र सहित वर्णन निम्न प्रकार है -

1. SSS सर्वांगसमता नियम ( Side-Side-Side Rule ) :-

यदि एक त्रिभुज की तीनों भुजाएँ क्रमशः किसी दूसरे त्रिभुज की संगत भुजाओं के बराबर हो , तो दोनों त्रिभुज सर्वांगसम होते है इसे त्रिभुज की सर्वांगसमता का भुजा-भुजा-भुजा नियम भी कहते है |

उदाहरण -

∆ABC तथा ∆PQR में
AB = RP = 3.5cm [ भुजा ]
BC = PQ = 7.1cm [ भुजा ]
AC = QR = 5cm [ भुजा ]
SSS नियम से
∆ABC ≌ ∆PQR

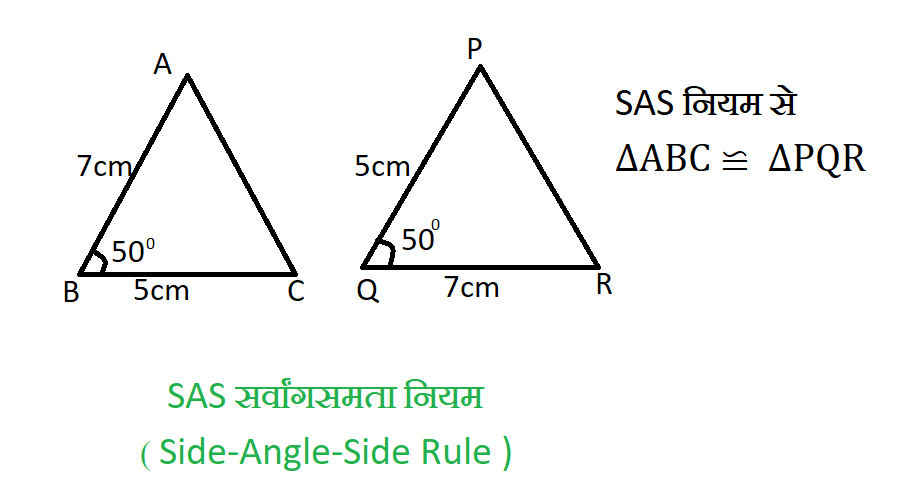
2. SAS सर्वांगसमता नियम ( Side-Angle-Side Rule ) :-

यदि एक त्रिभुज की दो भुजाएँ और उनके अंतर्गत कोण दूसरे त्रिभुज की संगत दो भुजाओं और उनके अंतर्गत कोण के बराबर हो , तो ये त्रिभुज सर्वांगसम होते है इसे त्रिभुज की सर्वांगसमता का भुजा-कोण-भुजा नियम भी कहते है |

उदाहरण -

∆ABC तथा ∆PQR में
AB = QR = 7cm [ भुजा ]
∠ABC = ∠PQR = 50° [ कोण ]
BC = PQ = 5cm [ भुजा ]
SAS नियम से
∆ABC ≌ ∆PQR

3. ASA सर्वांगसमता नियम ( Angle-Side-Side Rule ) :-

यदि एक त्रिभुज के दो कोण और उनके अंतर्गत भुजा , किसी दूसरे त्रिभुज के संगत दो कोणों और अंतर्गत भुजा के बराबर हो तो वे त्रिभुज सर्वांगसम होते है इसे त्रिभुज की सर्वांगसमता का कोण-भुजा-कोण नियम भी कहते है |

उदाहरण -

∆AOC तथा ∆BOD में
∠ACO = ∠BDO = 70° [ कोण ]
AC = BD = 3cm [ भुजा ]
∠AOC = ∠BOD = 30° [ कोण ]
ASA नियम से
∆AOC ≌ ∆BOD

4. समकोण त्रिभुज में RHS सर्वांगसमता नियम :-

किसी समकोण त्रिभुज का कर्ण और एक भुजा क्रमशः किसी दूसरे समकोण त्रिभुज के कर्ण और एक भुजा के बराबर हो तो वे त्रिभुज सर्वांगसम होते है |
इसे ही समकोण त्रिभुज में RHS सर्वांगसमता नियम कहते है |

उदाहरण :-

यहाँ RHS में R समकोण ( Right Angle ) H कर्ण ( Hypotenuse ) तथा S-भुजा (Side) को दर्शाता है |
∆PQR तथा ∆ABC में
∠QPR = ∠CBA = 90° [ समकोण ]
QR = AC = 8cm [ कर्ण भुजा ]
PR = AB = 3cm [ भुजा ]
RHS नियम से
∆PQR ≌ ∆ABC

सर्वांगसमता के महत्वपूर्ण तथ्य या बिंदु :-

1. सर्वांगसम वस्तुएँ एक - दूसरे की प्रतिलिपियाँ होती है |
2. दो त्रिभुजों में AAA सर्वांगसमता ( कोण-कोण-कोण नियम ) "नहीं" होती है |
3. यह आवश्यक नहीं है कि बराबर संगत कोणों के दो त्रिभुज सर्वांगसम हो | ऐसे सुमेलनों में इनमे से एक , दूसरे की बढ़ी हुई प्रतिलिपि हो सकती हैं |
4. दो त्रिभुज सर्वांगसम होंगे यदि वे एक - दूसरे की एक जैसी प्रतिलिपि हो |

समरूपता ( Similarity ) क्या है / समरूपता किसे कहते है ?

समरूपता की परिभाषा के अनुसार , दो ऐसी आकृतियाँ जिनके आकार समान हो परन्तु समान आमाप होना आवश्यक न हो , समरूप आकृतियाँ ( Similar figures ) कहलाती है यह गुणधर्म समरूपता ( Similarity ) कहलाता है |
इस लेख में हम समरूप त्रिभुज के बारें में जानेंगे |

समरूपता के उदाहरण

:- 1. सभी वृत्त समरूप होते है |
2. एक ही आकार के त्रिभुज

समरूपता का चिन्ह :-

यदि ∆ABC तथा ∆PQR परस्पर समरूप है तो उन्हें निम्न चिन्ह से व्यक्त करते है -
∆ABC ∼ ∆PQR

त्रिभुजों की समरूपता के नियम या शर्तें:-

दो त्रिभुज समरूप होते है यदि -
1. उनके संगत कोण बराबर हो |
2. उनकी संगत भुजाएँ एक ही अनुपात में हो ( अर्थात् समानुपाती हों )
दो त्रिभुजों की समरूपता के लिए ये दोनों नियम संतुष्ट होने चाहिए |

समानकोणिक त्रिभुज ( Equiangular Triangles ) किसे कहते है ?

यदि दो त्रिभुजों के संगत कोण बराबर हो , तो वे समानकोणिक त्रिभुज कहलाते है |

गणितज्ञ थैल्स के अनुसार " दो समानकोणिक त्रिभुजों में उनकी संगत भुजाओं का अनुपात सदैव समान रहता है | " इसे समानुपातिकता या थैल्स प्रमेय कहा जाता है

समरूपता का अर्थ :-

समरूपता का अर्थ " आकृतियों के आकार का समान " होने से है |

त्रिभुजों की समरूपता का उदाहरण :-

माना दो त्रिभुज ∆ABC तथा ∆DEF है जिनके संगत कोण बराबर है तथा संगत भुजाएँ एक ही अनुपात में है -

∆ABC तथा ∆DEF में
1. ∠A = ∠D , ∠B = ∠E , ∠C = ∠F

AB / DE

BC / EF

CA / FD

समरूपता की शर्त के अनुसार

∆ABC ∼ ∆DEF

Note :- त्रिभुजों की समरूपता तथा सर्वांगसमता को सांकेतिक रूप से व्यक्त करने के लिए , उनके शीर्षों की संगतताओं को सही क्रम में लिखा जाना चाहिए |

त्रिभुजों की समरूपता के नियम / प्रतिबन्ध / कसौटियाँ / प्रकार :-

त्रिभुजों की समरूपता के मुख्यतः तीन नियम या प्रतिबन्ध सूत्र है जिनका परिभाषा , उदाहरण एवं चित्र सहित वर्णन निम्न प्रकार है -

1. AAA समरूपता नियम ( Angle-Angle-Angle Rule ) :-

यदि एक त्रिभुज के दो कोण एक अन्य त्रिभुज के क्रमशः दो कोणों के बराबर हों , तो दोनों त्रिभुज समरूप होते है |
इसे दो त्रिभुजों की समरूपता की AAA कसौटी ( कोण-कोण-कोण नियम ) कहा जाता है |

∆ABC तथा ∆DEF में

∠A = ∠D = 50° ( कोण )
∠C = ∠F = 60° ( कोण )
∠B = ∠E = 70° ( कोण )
AAA समरूपता नियम से

∆ABC ∼ ∆DEF

तब

AB / DE

BC / EF

CA / FD

2. SSS समरूपता नियम :-

यदि दो त्रिभुजों में एक त्रिभुज की भुजाएँ दूसरे त्रिभुज की भुजाओं के समानुपाती ( एक ही अनुपात में ) हो तो उनके संगत कोण बराबर होते है , और इसलिए दोनों त्रिभुज समरूप होते है |
इस कसौटी को दो त्रिभुजों की समरूपता की SSS ( भुजा-भुजा-भुजा ) कसौटी कहा जाता है |

∆ABC तथा ∆DEF में

यहाँ

AB / DE

BC / EF

CA / FD

तब ∠A = ∠D , ∠B = ∠E , ∠C = ∠F होगा

SSS समरूपता नियम से

∆ABC ∼ ∆DEF

3. SAS समरूपता नियम :-

यदि एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा इन कोणों को अंतर्गत करने वाली भुजाएँ समानुपाती हो , तो दोनों त्रिभुज समरूप होते है |
इस कसौटी को दो त्रिभुजों की समरूपता की SAS ( भुजा-कोण-भुजा ) कसौटी कहा जाता है |

∆ABC तथा ∆DEF में
∠A = ∠D = 60°

तथा

AB / DE

AC / DF

SAS समरूपता नियम से

∆ABC ∼ ∆DEF

समरूप त्रिभुजों के क्षेत्रफल :-

दो समरूप त्रिभुजों के क्षैत्रफलों का अनुपात इनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है |

उदाहरण -

यहाँ ∆ABC ∼ ∆DEF

∆ABC का क्षैत्रफल / ∆DEF का क्षैत्रफल

= [

AB / DE

]2 = [

BC / EF

]2 = [

CA / FD

समकोण त्रिभुज में समरूपता :-

यदि किसी समकोण त्रिभुज के समकोण वाले शीर्ष से कर्ण पर लम्ब डाला जाए तो इस लम्ब के दोनों ओर बने त्रिभुज सम्पूर्ण त्रिभुज के समरूप होते है तथा परस्पर भी समरूप होते है |

उदाहरण :-

यहाँ ∆ADB ∼ ∆ABC ∼ ∆BDC

दो समकोण त्रिभुजों में RHS समरूपता कसौटी :-

यदि दो समकोण त्रिभुजों में एक त्रिभुज का कर्ण तथा एक भुजा , दूसरे त्रिभुज के कर्ण तथा एक भुजा के समानुपाती हो तो दोनों त्रिभुज समरूप होते है |
इसे RHS समरूपता कसौटी कहा जा सकता है |

उदाहरण :-

समकोण ∆ABC तथा ∆PQR में

तथा

AC / BC

PR / QR

( दिया है )

RHS समरूपता नियम से

∆ABC ∼ ∆PQR

समरूप त्रिभुजों पर आधारित महत्वपूर्ण प्रमेय :-

प्रमेय - 1 :- यदि किसी त्रिभुज कि एक भुजा के समांतर अन्य दो भुजाओं को भिन्न - भिन्न बिन्दुओं पर प्रतिच्छेद करने के लिए एक रेखा खीचीं जाए , तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती है |

∆ABC में भुजा BC के समांतर रेखा DE है |

तब

AD / DB

AE / EC

प्रमेय - 2 :- यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करें तो वह तीसरी भुजा के समांतर होती है |

दिया है -

AD / DB

AE / EC

तो DE || BC

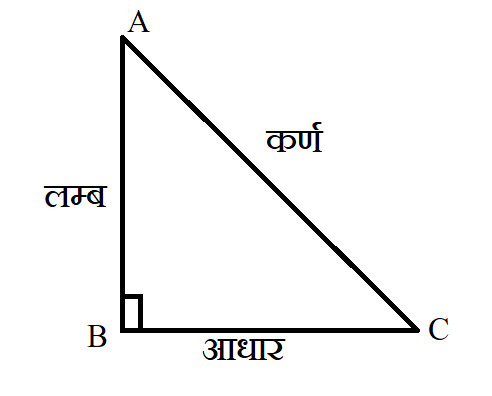
प्रमेय - 3 :- समकोण त्रिभुज के लिए पाइथागोरस प्रमेय :- एक समकोण त्रिभुज में कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है |

पाइथागोरस प्रमेय से -
कर्ण² = आधार² + लम्ब²
AC² = BC² + AB²

प्रमेय - 4 :- यदि किसी त्रिभुज की एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो तो पहली भुजा का सम्मुख कोण समकोण होता है |

∆ABC में
AC² = BC² + AB² है तो
∠B = 90°

सर्वांगसमता तथा समरूपता में अंतर ( Difference between Congruency and Similarity ) :-

क्रम संख्या	सर्वांगसमता ( Congruency )	समरूपता ( Similarity )
1.	वे आकृतियाँ जिनके समान आकार और समान माप है , सर्वांगसम आकृतियाँ कहलाती है \| यह गुणधर्म सर्वांगसमता कहलाती है \|	दो ऐसी आकृतियाँ जिनके आकार समान हो परन्तु समान आमाप होना आवश्यक न हो , समरूप आकृतियाँ कहलाती है \| यह गुणधर्म समरूपता कहलाता है \|
2.	सभी सर्वांगसम आकृतियाँ समरूप होती है \|	परन्तु सभी समरूप आकृतियों का सर्वांगसम होना आवश्यक नही है \|
3.	सर्वांगसमता का चिन्ह ≌ होता है	समरूपता का चिन्ह ∼ होता है \|
4.	दो त्रिभुज सर्वांगसम होते है यदि वे एक - दूसरे की प्रतिलिपियाँ ( Photo Copy ) हो और एक को दूसरे के ऊपर रखे जाने पर वे एक - दूसरे को आपस में पूर्णतया ढक लें \|	दो त्रिभुज समरूप होते है यदि उनके संगत कोण बराबर हो तथा उनकी संगत भुजाएँ एक ही अनुपात में हो \|
5.	त्रिभुजों में सर्वांगसमता के नियम - SSS,SAS,ASA,RHS	त्रिभुजों में समरूपता के नियम - AAA,SSS,SAS,RHS
6.	दो त्रिभुजों में AAA सर्वांगसमता नहीं होती है	दो त्रिभुजों में AAA समरूपता होती है
7.	उदाहरण :- एक ही कंपनी के शेविंग ब्लेड एक ही पैकेट के बिस्कुट , एक ही माप और आकार के त्रिभुज	उदाहरण :- सभी वृत्त समरूप होते है \| सभी वर्ग समरूप होते है एक ही आकार के त्रिभुज

सर्वांगसमता और समरूपता शब्दावली :-

Sarvangsamta meaning / translate in English :- Congruency ( सर्वांगसमता )

Sarvangsamta in hindi :- सर्वांगसमता ( Congruency )

Samrupta meaning / translate in English :- Similarity (समरूपता)

Samrupta meaning in hindi :- समरूपता (Similarity)