बहुपद की परिभाषा, सूत्र , प्रकार एवं उदाहरण | Mcqs Questions | PDF Download |

इस लेख में हमारे द्वारा बहुपद की परिभाषा,सूत्र,प्रकार एवं उदाहरण और महत्वपूर्ण प्रश्नोतरी दिए गए है जो कक्षा 8 से 10,कक्षा 9 NCERT बहुपद notes in hindi तथा 11 एवं 12 के लिए अतिमहत्वपूर्ण है | कक्षा 8 से 10 NCERT के लिए तो यह लेख बहुत ही फायदेमंद है | आप हमे नीचे comment करके बता सकते है कि आपको यह लेख कैसा लगा |

{tocify} $title={Table of Contents}

Bahupad ki paribhasha , udaharan, sutra , prakar, question and answer :-

बहुपद क्या है / बहुपद किसे कहते है ?

बहुपद की परिभाषा के अनुसार , चर एवं अचर पदों के समूह से बनने वाले व्यंजक को बहुपद कहते है |
किसी बहुपदीय व्यंजक में धनात्मक तथा ऋणात्मक चिन्ह दोनों शामिल हो सकते है |

---

Bahupad Meaning in English - Polynomial

Polynomial Meaning/translate in Hindi - बहुपद

---

बहुपद के उदाहरण ( Bahupad Examples ) :-

4𝓍 + 3
2𝓍² + 3𝓍 + 5 आदि |

---

बहुपद की घात ( Degree of Polynomial ) किसे कहते है ? :-

बहुपद की घात की परिभाषा के अनुसार, चर 𝓍 के बहुपद P(𝓍) में 𝓍 की उच्चतम घात ( Power ) , बहुपद की घात ( Degree) कहलाती है |
उदाहरण :- 5𝓍 + 3 में चर 𝓍 की उच्चतम घात 1 है |
3𝓍³ + 4𝓍 + 5 में चर 𝓍 की उच्चतम घात 3 है |

---

बहुपद का शुन्यक ( Zeros) किसे कहते है ?

यदि P(𝓍) ; 𝓍 में कोई बहुपद है और K कोई वास्तविक संख्या है , तो P(𝓍) में 𝓍 को k से प्रतिस्थापित करने पर प्राप्त वास्तविक संख्या P(𝓍) का 𝓍 = k पर मान कहलाती है और इसे P(k) से निरुपित करते है |

अधिक व्यापक रूप में , एक वास्तविक संख्या k बहुपद P(𝓍) की शुन्यक कहलाती है यदि P(𝓍) = 0 हो |

साधारण शब्दों में कहा जाए तो , वह वास्तविक संख्या जिसके लिए किसी बहुपद का मान शून्य प्राप्त हो , उस वास्तविक संख्या को बहुपद का शून्यक कहते है |
उदाहरणार्थ :- 4𝓍 - 8 𝓍 = 2 रखने पर 4(2) - 8 = 8 - 8 = 0 अत: 2, बहुपद 4𝓍 - 8 का एक शून्यक है |

---

बहुपद की पहचान कैसे की जाती है ?

यहाँ हम सीखेंगे कि बहुपद कैसे पहचाने ? कोई भी गणितीय व्यंजक एक बहुपद होगा यदि उसके सभी पदों की घात एक धनात्मक पूर्णांक हो | यदि किसी व्यंजक की घात , भिन्न , ऋणात्मक पूर्णांक या अपरिमेय संख्या हो तो वह व्यंजक बहुपद नहीं कहलाएगा |

---

बहुपद की पहचान करने के उदाहरण :-

(1) 2𝓍² + 𝓍 + 3 , एक बहुपद है क्योकिं 𝓍 की घात धनात्मक है | (2) y² + √5 , एक बहुपद है क्योकिं y की घात धनात्मक है | (3) √z + √5 , बहुपद नहीं है क्योकिं z की घात एक भिन्न है | (4) 𝓍^-1 + 2 , बहुपद नही है क्योकि 𝓍 की घात ऋणात्मक है |

---

बहुपद के प्रकार ( Bahupad ke prakar) :-

यहाँ हम जानेगें की बहुपद कितने प्रकार के होते है -

बीजीय बहुपद (Algebraic Polynomial) किसे कहते है ?

बीजीय बहुपद की परिभाषा के अनुसार , चर एवं अचर बहुपद के सम्मिलित रूप को बीजीय बहुपद कहते है |

---

बीजीय बहुपद के उदाहरण :-

𝓍 + 5 , -y + 2 आदि |

---

बीजीय बहुपद के प्रकार :-

बीजीय बहुपद मुख्यतः दो प्रकार के होते है जिनका परिभाषा एवं उदाहरण सहित वर्णन निम्न प्रकार है -

(1) अचर बहुपद (Achar Bahupad) :-

बहुपद का वह पद जिसका मान हमेशा स्थिर रहें , उसे अचर बहुपद कहते है |
अचर बहुपद के उदाहरण :- बहुपद 𝓍 + 5 में 5 एक अचर बहुपद है क्योकि इसका मान सदैव स्थिर रहता है | अचर बहुपद की घात शून्य होती है |

(2) चर बहुपद (Char Bahupad) :-

बहुपद का वह पद जिसका मान हमेशा परिवर्तित होता रहता है इसे चर बहुपद कहते है |
चर बहुपद के उदाहरण :- 𝓍² + 3𝓍 + 4 चर बहुपद को अंग्रेजी के अक्षर ( 𝓍 , y , z ) द्वारा व्यक्त किया जाता है |

(2) घात के आधार पर बहुपद :-

बहुपद को घात के आधार पर मुख्यतः चार भागों में बांटा गया है जिनका परिभाषा एवं उदाहरण सहित वर्णन निम्न प्रकार है -

1. रैखिक बहुपद ( Linear Polynomial) किसे कहते है ?

रेखिक बहुपद की परिभाषा के अनुसार , वह बहुपद जिसमे चर की अधिकतम घात 1 हो , रैखिक बहुपद कहलाता है |

रैखिक बहुपद के उदाहरण :-

2𝓍 - 3 y + √5 आदि |

रैखिक बहुपद का व्यापक रूप या मानक रूप :-

a𝓍 + b जहाँ a,b :- वास्तविक संख्याएँ तथा a ≠ 0 जब हम रैखिक बहुपद को शून्य के बराबर रख देते है तो हमें रैखिक समीकरण प्राप्त होता है |
a𝓍 + b = 0 उपरोक्त समीकरण रैखिक समीकरण का मानक रूप कहलाता है |

रैखिक बहुपद में शून्यको की संख्या :-

रैखिक बहुपद का केवल एक ही शुन्यक प्राप्त होता है |

रैखिक बहुपद का शून्यक (Zeros) का सूत्र :-

रैखिक बहुपद a𝓍 + b का शुन्यक =

-b / a

=

-(अचर पद) / 𝓍 का गुणांक

---

(2) द्विघात बहुपद ( Quadratic Polynomial) किसे कहते है ?

द्विघात बहुपद की परिभाषा के अनुसार , वह बहुपद जिसमें चर की अधिकतम घात 2 हो , द्विघात बहुपद कहलाता है |

द्विघात बहुपद के उदाहरण :-

y² - 2 2𝓍² + 3𝓍 + 5 आदि |

द्विघात बहुपद का मानक रूप या व्यापक रूप :-

a𝓍² + b𝓍 + c जहाँ a,b,c :- वास्तविक संख्याएँ तथा a ≠ 0 जब हम द्विघात बहुपद a𝓍² + b𝓍 + c को शून्य के बराबर रख देते है तो हमें द्विघात समीकरण प्राप्त होता है | a𝓍² + b𝓍 + c = 0 उपरोक्त समीकरण द्विघात समीकरण का मानक रूप कहलाता है |

द्विघात बहुपद के शुन्यंको की संख्या :-

द्विघात बहुपद में शुन्यांकों की संख्या 2 होती है जिन्हें α तथा β से व्यक्त किया जाता है |

द्विघात बहुपद के शुन्यंको का योग का सूत्र :-

शुन्यंको का योग (α + β) =

-b / a

=

-( 𝓍 का गुणांक ) / 𝓍² का गुणांक

द्विघात बहुपद के शुन्यंको का गुणनफल का सूत्र :-

शुन्यंको का गुणनफल (α.β) =

c / a

=

अचर पद / 𝓍² का गुणांक

द्विघात बहुपद का सूत्र ( Dwighat bahupad formula in hindi ) :-

यदि द्विघात बहुपद के शुन्यकों का योग (α + β) तथा शुन्यंको का गुणनफल (α.β) ज्ञात हो तो द्विघात बहुपद निम्न सूत्र से प्राप्त किया जा सकता है - द्विघात बहुपद = 𝓍² - ( शुन्यंको का योग )𝓍 + ( शुन्यंको का गुणनफल ) = 𝓍² - (α + β)𝓍 + (α.β) साधारण शब्दों में इसे " द्विघात बहुपद बनाने का सूत्र " कहते है |

---

(3) त्रिघात बहुपद ( Cubic Polynomial ) किसे कहते है ?

त्रिघात बहुपद की परिभाषा के अनुसार , वह बहुपद जिसमें चर की अधिकतम घात 3 हो , त्रिघात बहुपद कहलाता है |

त्रिघात बहुपद के उदाहरण :-

𝓍³ -𝓍³ + 2 3𝓍³ - 2𝓍² + 𝓍 - 1 आदि |

त्रिघात बहुपद का मानक रूप या व्यापक रूप :-

a𝓍³ + b𝓍² + c𝓍 + d = 0 जहाँ a,b,c,d :- वास्तविक संख्याएँ
तथा a ≠ 0
जब हम त्रिघात बहुपद a𝓍³ + b𝓍² + c𝓍 + d को शून्य के बराबर रख देते है तो हमें त्रिघात बहुपद प्राप्त होता है | a𝓍³ + b𝓍² + c𝓍 + d = 0 उपरोक्त समीकरण त्रिघात समीकरण का मानक रूप कहलाता है |

त्रिघात बहुपद के शुन्यंको की संख्या :-

त्रिघात बहुपद में शुन्यांकों की संख्या 3 होती है जिन्हें α,β तथा γ से व्यक्त किया जाता है |

त्रिघात बहुपद के शुन्यंको का योग का सूत्र :-

शुन्यंको का योग (α + β + γ ) =

-( 𝓍² का गुणांक ) / 𝓍³ का गुणांक

α + β + γ =

-b / a

त्रिघात बहुपद के शुन्यंको का गुणनफल का सूत्र :-

शुन्यंको का गुणनफल (α.β.γ) =

- (अचर पद ) / 𝓍³ का गुणांक

α.β.γ =

- d / a

तथा α.β + β.γ + γ.α =

c / a

त्रिघात बहुपद का सूत्र ( Trighat Bahupad Formula) :-

यदि हमें त्रिघात बहुपद के तीनों शुन्यक α , β तथा ज्ञात हो तो हम त्रिघात बहुपद निम्न सूत्र से प्राप्त कर सकते है - त्रिघात बहुपद = 𝓍³ - (α + β + γ )𝓍² + ( α.β + βγ + γα)𝓍 - (α.β.γ)

---

(4) शून्य बहुपद (Zero Polynomials) किसे कहते है ?

शून्य बहुपद की परिभाषा के अनुसार , बहुपद p(𝓍) = 0 को शून्य बहुपद कहते है | शून्य बहुपद की घात बतायी नही जाती है |
सामान्यत: इसे 0 बहुपद कहा जाता है |

---

पदों के आधार पर बहुपद का वर्गीकरण :-

पद के आधार पर बहुपद मुख्यतः तीन प्रकार के होते है जिनका परिभाषा एवं उदाहरण सहित वर्णन निम्न प्रकार है -

(1) एकपदी बहुपद ( Monomial) किसे कहते है ?

एकपदी बहुपद की परिभाषा के अनुसार , वह बहुपद जिसमें पद की संख्या 1 हो , एकपदी बहुपद कहलाता है |

एकपदी बहुपद के उदाहरण :-

𝓍 , 𝓍³ , 5 आदि |

(2) द्विपदी बहुपद ( Binomial) किसे कहते है ?

द्विपदी बहुपद की परिभाषा के अनुसार , वह बहुपद जिसमें पदों की संख्या 2 हो , द्विपदी बहुपद कहलाता है |

द्विपदी बहुपद के उदाहरण :-

𝓍 + 8 , 𝓍² - 3 , 𝓍⁴ + 3 आदि |

(3) त्रिपदी बहुपद ( Trinomial ) किसे कहते है ?

त्रिपदी बहुपद की परिभाषा के अनुसार , वह बहुपद जिसमें पदों की संख्या तीन हो , त्रिपदी बहुपद कहलाता है |

त्रिपदी बहुपद के उदाहरण :-

𝓍² + 3𝓍 + 8 , 3𝓍³ + 2𝓍² + 5 आदि |

बहुपदों के लिए विभाजन एल्गोरिथम :-

विभाजन एल्गोरिथम के अनुसार, दिए गए बहुपद p(𝓍) और शुन्येतर बहुपद g(𝓍) के लिए दो ऐसे बहुपदों q(𝓍) तथा r(𝓍) का अस्तित्व है कि - p(𝓍) = g(𝓍).q(𝓍) + r(𝓍) जहाँ r(𝓍) = 0 या घात r(𝓍) < घात g(𝓍) है |

बहुपद की भाग विधि :-

इसे बहुपद वाला भाग भी कहते है |
यहाँ हम बहुपदों के विभाजन को एक उदाहरण की सहायता से समझेगें और यह भी समझेंगे कि बहुपद का भाग कैसे करे |

चरण - I :- सर्वप्रथम भाजक एवं भाज्य के पदों को घटाती हुई घातों के क्रम में व्यवस्थित करते है |

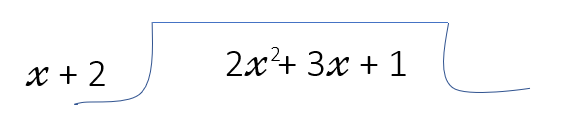
चरण - II :- भाज्य के प्रथम पद ( 2𝓍²) को भाजक के प्रथम पद ( 𝓍 ) से भाग देंगे ( 2𝓍² / 𝓍 = 2𝓍 ) प्राप्त भागफल 2𝓍 को सम्पूर्ण भाजक से गुणा करेंगे | 2𝓍 ( 𝓍 + 2 ) = 2𝓍² + 4𝓍

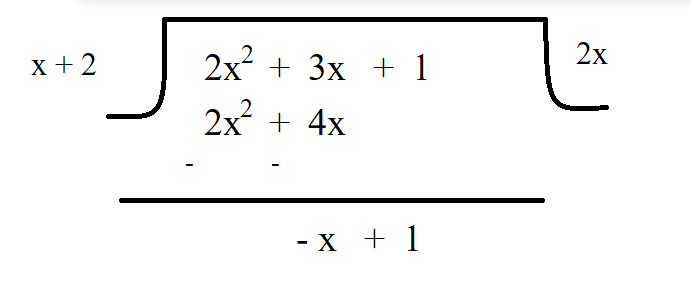
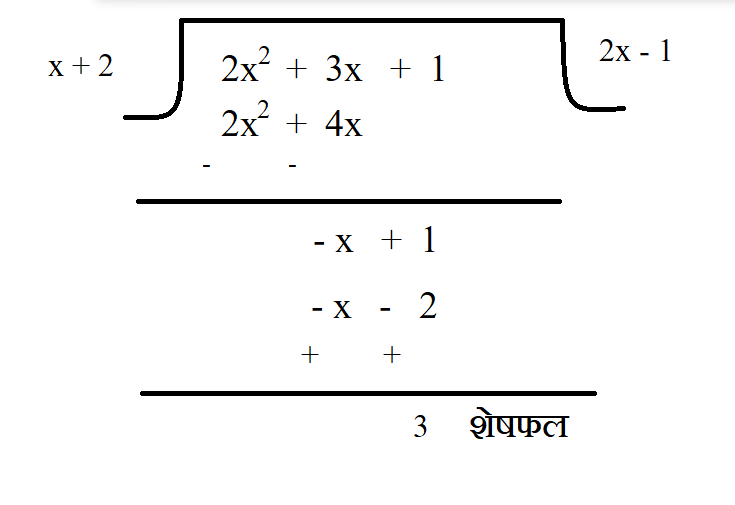
चरण - III :- अब पुन: -𝓍 + 1 के प्रथम पद ( -𝓍 ) में भाजक के प्रथम पद ( 𝓍 ) से भाग करेंगे ( -𝓍/y = -1)
प्राप्त भागफल -1 को सम्पूर्ण भाजक से गुणा करेंगे | -1 ( 𝓍 + 2 ) = - 𝓍 - 2

बहुपद से सम्बंधित प्रश्नोतरी ( Bahupad Question and Answer ) :-

(1) नीचे दिए गए रैखिक बहुपदों के शून्यक ज्ञात कीजिए |

(1) 𝓍 + 5
रैखिक बहुपद 𝓍 + 5 का शून्यक = -( अचर पद ) / 𝓍 का गुणांक = - (5) / 1 = -5

(2) 4𝓍 + 3
रैखिक बहुपद 4𝓍 + 3 का शून्यक = -b/a = -3/4

(3) 8𝓍 + 14
रैखिक बहुपद 8𝓍 + 14 का शुन्यक = -b/a = -14/8 = -7/4

(4) 2𝓍 + 5
रैखिक बहुपद 2𝓍 + 5 का शुन्यक = -b/a = -5/2

(2) नीचे दिए गए द्विघात बहुपदों के शुन्यक ज्ञात कीजिए -

(1) 𝓍² - 3 द्विघात बहुपद 𝓍² - 3 के शुन्यक 𝓍² - 3 = 𝓍² - (√5)2 (𝓍 - √3) (𝓍 + √3) अत: बहुपद 𝓍² - 3 के शुन्यक √3 और -√3 है |

(2) 𝓍² - 8𝓍 + 12 द्विघात बहुपद 𝓍² - 8𝓍 + 12 के शुन्यक 𝓍² - 8𝓍 + 12 = 𝓍² - 2𝓍 - 6𝓍 + 12 𝓍(𝓍 - 2) - 6(𝓍 - 2) (𝓍 - 2) (𝓍 - 6) अत: बहुपद 𝓍² - 8𝓍 + 12 के शुन्यक 2 और 6 है |

बहुपद Y² - 5Y + 6 के गुणनखंड कीजिए -

Y² - 5Y + 16 = Y² - 2Y - 3Y + 6 Y(Y - 2) - 3(Y - 2) (Y - 3) (Y - 2) अत: बहुपद Y² - 5Y + 6 के गुणनखंड (Y - 3) और (Y - 2) है |

बहुपद 12𝓍² - 7𝓍 + 1 के गुणनखंड कीजिए |

12𝓍² - 7𝓍 + 1 = 12𝓍² - 3𝓍 - 4𝓍 + 1 = 3𝓍 ( 4𝓍 - 1 ) -1 ( 4𝓍 - 1 ) = ( 3𝓍 - 1 ) ( 4𝓍 - 1 ) अत: बहुपद 12𝓍² - 7𝓍 + 1 के गुणनखंड ( 3𝓍 - 1 ) ( 4𝓍 - 1 ) है |

नीचे दिए गए बहुपद की घात लिखिए |

1. 5𝓍³ + 4𝓍² + 7𝓍
बहुपद 5𝓍³ + 4𝓍² + 7𝓍 की घात = 3

2. 𝓍² + 2𝓍 + 1
बहुपद 𝓍² + 2𝓍 + 1 की घात = 2

शेषफल प्रमेय ( Remainder Theorem ) किसे कहते है ?

शेषफल प्रमेय की परिभाषा के अनुसार , माना कि P(𝓍) एक से अधिक या एक के बराबर घात वाला एक बहुपद है और मानाकि a कोई वास्तविक संख्या है यदि P(𝓍) को रैखिक बहुपद (𝓍 - a) से भाग दिया जाए , तो शेषफल P(a) होता है |

शेषफल प्रमेय पर आधारित उदाहरण :-

𝓍⁴ + 𝓍³ + 𝓍² + 𝓍 + 1 को ( 𝓍 - 1 ) से भाग देने पर प्राप्त शेषफल ज्ञात कीजिए |
बहुपद 𝓍 - 1 का शून्यक 1 है |
तब P(𝓍) = 𝓍⁴ + 𝓍³ + 𝓍² + 𝓍 + 1 P(1) = (1)⁴ + (1)³ + (1)² + 1 + 1 = 2 अत: शेषफल 2 होगा |

गुणनखंड प्रमेय ( Factor Theorem) किसे कहते है ?

गुणनखंड प्रमेय की परिभाषा के अनुसार , यदि P(𝓍) घात n 1 वाला एक बहुपद हो और a कोई वास्तविक संख्या हो , तो -
𝓍 - a , P(𝓍) का एक गुणनखंड होता है यदि P(a) = 0 हो , और
P(a) = 0 होता है , यदि ( 𝓍 - a) , P(𝓍) का एक गुणनखंड हो |

गुणनखंड प्रमेय पर आधारित उदाहरण :-

जाँच कीजिए कि 𝓍 + 2 , बहुपद 2𝓍 + 4 का एक गुणनखंड है या नही ?
𝓍 + 2 का शून्यक -2 है |
तब P(𝓍) = 2𝓍 + 4
P(-2) = 2(-2) + 4 = 0
अत: गुणनखंड प्रमेय के अनुसार 𝓍 + 2 बहुपद 2𝓍 + 4 का एक गुणनखंड है |

महत्वपूर्ण बीजीय सर्वसमिकाएँ (सूत्र) :-

1. (𝓍 + y)² = 𝓍² + 2𝓍y + y²

2. (𝓍 - y)² = 𝓍² - 2𝓍y + y²

3. 𝓍² - y² = (𝓍 - y) (𝓍 + y)

4. (𝓍 + a) (𝓍 + b) = 𝓍² + (a + b)𝓍 + ab

5. (𝓍 + y + z)² = 𝓍² + y² + z² + 2𝓍y + 2yz + 2z𝓍

6. (𝓍 + y)³ = 𝓍³ + y³ + 3𝓍y(𝓍 + y)

7. (𝓍 - y)³ = 𝓍³ - y³ - 3𝓍y(𝓍 - y)

8. 𝓍³ + y³ + z³ - 3𝓍yz = ( 𝓍 + y + z) ( 𝓍² + y² + z² - 𝓍y - yz - z𝓍 )

बहुपद की परिभाषा,सूत्र,प्रकार एवं उदाहरण Download PDF

Download PDF

Download PDF
3.4 MB

Maths Notes की Free PDF यहां से Download करें

सभी बिषयवार Free PDF यहां से Download करें